Wintermute OTC年度报告:下半年交易量增长4倍,TradFi重新兴起
作者:
编译:Felix, PANews
2023年的加密市场经历了一系列的高峰和低谷。从年初的反弹,到年中的波动,最终以乐观的市场情绪结束(由现货ETF获批的预期推动)。在市场活动放缓时候,行业叙事转向了Build。去年,Wintermute专注于拓展OTC业务,开发新产品。
最新的里程碑包括Wintermute亚洲与CME的整合,场外期权产品的重大升级,以及正开发更多衍生产品。自去年11月推出以来,Wintermute亚洲的期权交易量达2.1亿美元,交易对手(Counterparties)对该产品的需求呈指数级增长。
新年之际,Wintermute分享了业务动态,并反思在2023年通过OTC观察到的一些趋势。
随着交易量转移到场外,OTC下半年交易量增长超400%
尽管2023年市场低迷,但Wintermute的所有垂直业务仍持续增长。现货市场方面,从上半年到下半年虽然场内总交易量下降约13%,但同期场外交易量增长超400%。
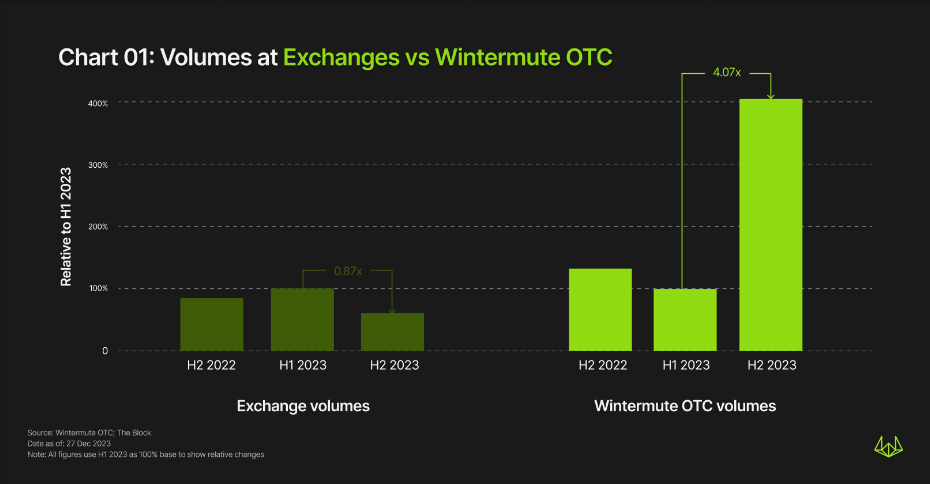
尽管2023年上半年与2022年下半年的场外交易数量相当,但2023年上半年场外交易量最初出现了下降。这表明,尽管交易规模有所减少,但交易对手的加密交易策略仍然坚定。随着2023年下半年市场回暖,交易活动显著增加,交易数量增长超过6倍,超2900万笔交易。在此期间,出现了单周最高场外交易量,超20亿美元。
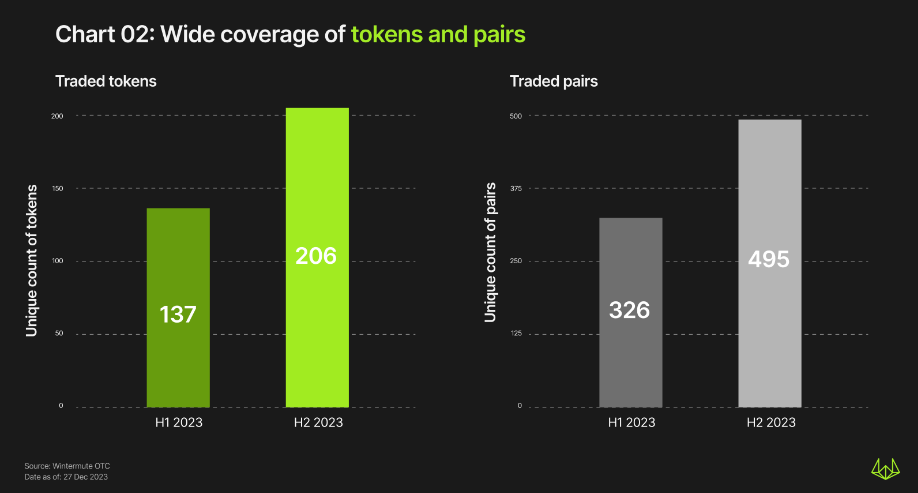
2023年Wintermute为206 种资产和495个交易对提供OTC交易。以下为Wintermute所观察到的整体资产交易趋势。
支付相关资产是交易量最大的加密货币类别,仅次于BTC和ETH
排除BTC和ETH(在所有时期内始终保持第一第二),支付相关资产的交易量和市场份额最高。支付相关资产的市场份额从2022年下半年的13%增长到2023年下半年的20%。
由于SEC-Ripple案裁决的结果,XRP在一定程度上推动了支付相关资产的增长。
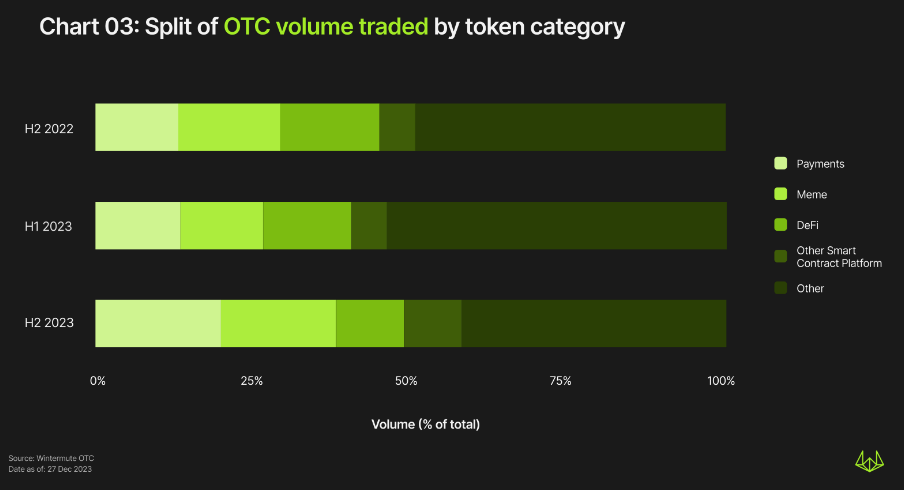
2023年下半年的其他类别包括Meme、DeFi和其他智能合约平台。这些类别的市场份额一直保持强劲,在2022年下半年和2023年下半年分别占37%和38%
L1和L2交易量继续增长,其中ETH和MATIC处于领先地位
L1资产的场外交易量遵循了场外交易量的总体趋势,从2022年下半年至 2023年上半年下降了约一半,然后在2023年下半年飙升了350%。交易量最大的是以太坊,占68%的市场份额。
值得注意的是,从2022年下半年到2023年下半年,以太坊的市场主导地位正逐步下降。
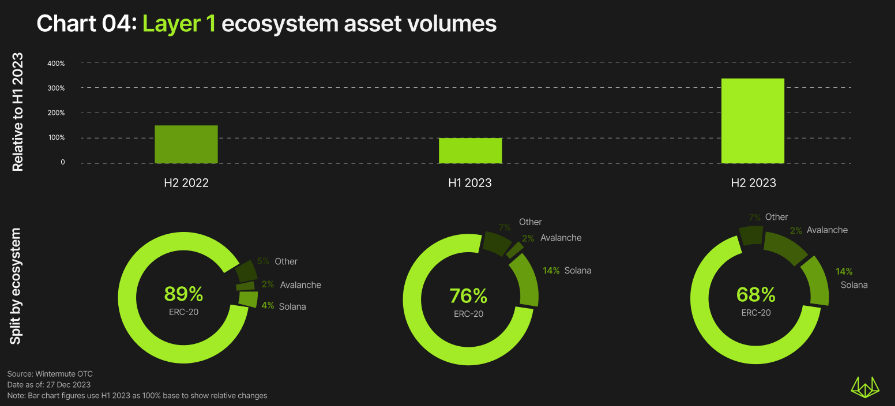
在2023年下半年,Solana、Avalanche、Cardano和Polkadot的交易量跻身前5。与以太坊相比,其他大多数L1资产在2023年上半年保持强劲,交易量有所增长,但Polkadot是一个例外,2023年上半年略有下降。
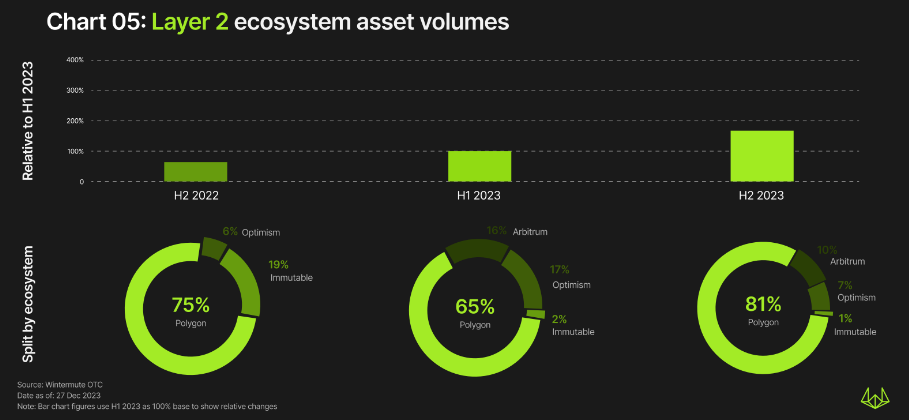
与L1相比,L2的交易活动减少约30倍,其中下降最多的是Polygon、Arbitrum和Optimism。但整体L2s的交易活动仍在持续增长,从2022年下半年到2023年下半年增长了约160%。
DeFi保持强劲,市场份额小幅增长,名义交易量大幅增长
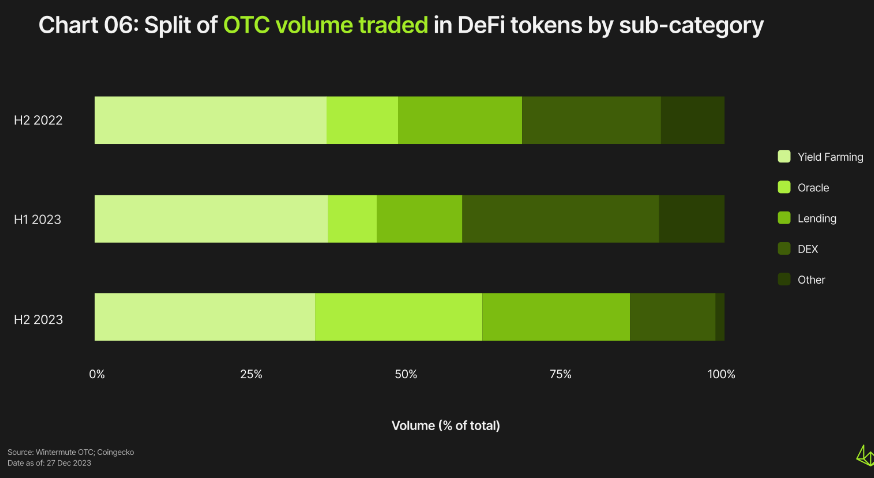
虽然从2022年下半年到2023年下半年,DeFi的义交易量增长了约7倍,但市场份额从16%降至11%。 在DeFi中,Yield Farming 的交易量最大,其次是预言机、借贷和DEX资产。
2023年全年Yield Farming的主导地位保持强劲,占整体DeFi交易量的35%左右,同期名义交易量增长了9倍以上。
从2022年下半年到2023年上半年,预言机相关资产的交易量(下降约30%)和市场份额(从11%降至8%)均略有下降,但在2023年下半年反弹,占整体DeFi交易量的26%。主要是抢夺了DEX资产份额。尽管DEX资产的名义交易量增长了3.4倍以上,但同期占DeFi的市场份额大幅下降(从31%降至13.5%)。
从2023年上半年到下半年,借贷相关资产的市场份额增加了10个百分点(从13%增加到23%)。
从2022年下半年到2023年上半年,衍生品资产的名义交易量最初飙升了10倍,市场份额从0.6%增长到6.9%。但到2023年下半年衍生品资产的市场份额降至0.5%。
TradFi重新兴起,并转向山寨币交易
就Crypto Native与TradFi的整体交易量而言,2022年下半年市场份额比例为81%:19%。在2023年下半年,TradFi重新出现,该比例调整至72%:28%。这表明TradFi的兴趣在2023年下半年再次回升,预计这种兴趣将持续增长到2024年。
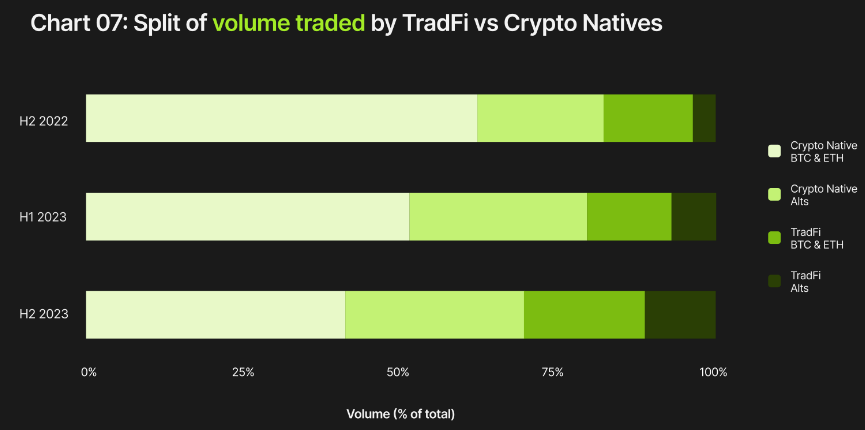
在每个时期,BTC和ETH无论在TradFi交易对手还是Crypto Native交易对手,其交易量中均占据主导地位。
但深入研究可以发现一些有趣的现象。2022年下半年,BTC和ETH在这两个交易对手类别中的主导地位显而易见,Crypto Natives的交易量市场份额合计为82.7%(BTC为44.9%,ETH为32.8%),TradFi的交易量市场份额为94%(BTC为62%,ETH为32%)。
这种现象在2023年下半年发生了变化,两个交易对手类别的BTC和ETH市场份额均下降了15%以上。Crypto Natives的交易量市场份额占65.3% (BTC为49.9%, ETH为15.4%),而TradFi的跌幅更大,为72.1% (BTC为50.3%,ETH为21.8%)。越来越多的非比特币、非以太坊的交易量按比例增长,表明市场对山寨币交易的兴趣日益浓厚。
这些趋势表明,TradFi的兴趣不仅重新兴起,而且其兴趣开始变得更加多元化。
除BTC和ETH外,Solana和支付相关资产中Crypto Native交易对手的交易量增长最块。相比之下,对于TradFi交易对手而言,DeFi相关资产增长最快。