技术范式共振，1.5万字详解人工智能+加密货币全景图

原文标题：《Understanding the Intersection of Crypto and AI》

原文作者：Lucas Tcheyan

原文编译：律动小工，BlockBeats

目录

介绍

核心观点术语解释

人工智能+加密货币全景图

去中心化计算

概述

去中心化计算垂直领域

通用计算

二级市场

去中心化机器学习训练

去中心化通用人工智能

构建用于

AI 模型的去中心化计算堆栈

其他去中心化产品

展望

智能合约与零知识机器学习（zkML）

零知识机器学习（zkML）

基础设施与工具

协处理器

应用

展望

人工智能代理

代理提供商

比特币和人工智能代理

展望

结论

介绍

区块链的出现可以说是计算机科学历史上最重要的进步之一。同时人工智能的发展将会，而且已经在我们的世界产生深远影响。如果说区块链技术提供了一种新的交易结算、数据存储和系统设计范例，人工智能则是计算、分析和内容生产的革命。这两个行业的创新正在解锁新的用例，这些用例可能会在未来几年加速两者的应用落地。本报告探讨了加密货币和人工智能的集成，重点关注试图弥合两者之间差别、利用两者力量的新用例。具体而言，本报告研究了去中心化计算协议、零知识机器学习（zkML）基础设施和人工智能代理的项目。

加密货币为人工智能提供了一个无需许可、无需信任、可组合的结算层。这解锁了更多用例，例如通过去中心化计算系统使硬件更容易获得，构建可以执行需要价值交换的复杂任务的人工智能代理，以及开发身份和来源解决方案来对抗女巫攻击和深伪技术（Deepfake）。人工智能为加密货币带来了许多好处，正如已经在 Web 2 中看到的那样。这包括通过大型语言模型（例如 ChatGPT 和 Copilot 的专门训练版本）增强了用户和开发者的用户体验（UX），以及显著提高智能合约功能和自动化的潜力。区块链是人工智能所需要的透明、数据丰富的环境。但区块链的计算能力也受到了限制，这是直接集成人工智能模型的主要障碍。

加密货币和人工智能的交叉点正在进行的实验和最终采用背后的驱动力，正是推动加密货币许多最有前景的用例的驱动力——一个无需许可、无需信任的协调层，更好地促进价值转移。鉴于其巨大潜力，该领域的参与者需要理解这两种技术相交的基本方式。

核心观点：

在不久的将来（6 个月到 1 年），加密货币和人工智能的集成将由人工智能应用程序主导，这些应用程序可以提高开发者的效率、智能合约的可审查性和安全性以及用户的可使用性。这些集成并非特定于加密货币，而是增强了链上开发者和用户的体验。

正如高性能 GPU 严重短缺一样，去中心化计算产品正在发展人工智能定制的 GPU 产品，这为其采用提供了有力支持。

用户体验和监管仍然是去中心化计算客户的障碍。然而，最近 OpenAI 的发展以及美国正在进行的监管审查突显了无需许可、抗审查、去中心化人工智能网络的价值主张。

链上人工智能整合，特别是能够使用人工智能模型的智能合约，需要改进 zkML 技术和其他验证链下计算的计算方法。缺乏全面的工具和开发人才以及高昂的成本是采用的障碍。

人工智能代理非常适合加密货币，用户（或代理本身）可以创建钱包以与其他服务、代理或个人进行交易。这在传统金融渠道下目前不可能实现。为了更广泛的采用，需要与非加密产品进行额外的集成。

术语解释：

人工智能（Artificial Intelligence）是利用计算和机器模仿人类的推理和问题解决能力。

神经网络（Neural Networks）是一种用于 AI 模型的训练方法。它们通过一系列算法层处理输入数据，不断优化直到产生所需的输出。神经网络由具有可修改权重的方程组成，可以修改权重以改变输出。它们可能需要大量的数据和计算来进行训练，以确保其输出准确。这是开发 AI 模型最常见的方式之一（例如，ChatGPT 使用基于 Transformer 的神经网络过程）。

训练（Training）是神经网络和其他 AI 模型开发的过程。它需要大量的数据来训练模型，以正确地解释输入并产生准确的输出。在训练过程中，模型方程的权重将不断修改，直到产生令人满意的输出为止。训练成本可能非常昂贵。例如，ChatGPT 使用数以万计的 GPU 来处理其数据。资源较少的团队通常依赖于像亚马逊网络服务（Amazon Web Services）、Azure 和谷歌云服务（Google Cloud Providers）等专用计算提供商。

推理（Inference）是实际使用 AI 模型获取输出或结果的过程（例如，使用 ChatGPT 撰写本报告大纲）。推理在训练过程中和最终产品中都会用到。由于计算成本的原因，即使在训练完成后，它们的运行成本也可能很高，但计算密集度低于训练。

零知识证明（Zero Knowledge Proofs，ZKP）允许在不透露基础信息的情况下验证声明。这在加密货币中有两个主要用途：1 隐私和 2 扩展性。对于隐私，这使用户能够进行交易而不泄露像钱包中有多少 ETH 这样的敏感信息。对于扩展性，它使得可以更快地在链上证明链下计算，而无需重新执行计算。这使得区块链和应用程序可以在链下运行计算，然后在链上进行验证。

人工智能+加密货币全景图

在人工智能和加密货币交汇的项目仍在开发所需的基础设施，以支持大规模的链上人工智能交互。

去中心化计算市场正在兴起，以提供大量的物理硬件，主要是GPU，用于训练和推理人工智能模型。这些双边市场连接了出租和寻求租用计算资源的人，促进了价值的转移和计算的验证。在去中心化计算中，正在出现几个子类别，提供了额外的功能。除了双边市场之外，本报告还将研究专门为可验证训练和微调输出的机器学习训练提供方，以及致力于连接计算和模型生成以实现人工通用智能的项目，也经常被称为智能激励网络。

zkML 是希望以经济有效且及时的方式在链上提供可验证模型输出的一个重点领域。这些项目主要使应用程序能够处理链下繁重的计算请求，然后在链上发布可验证的输出，证明链下工作是完整且准确的。zkML 在当前实例中既昂贵又耗时，但越来越多地被用作解决方案。这在 zkML 提供方和想要利用 AI 模型的 DeFi/游戏之间的集成数量不断增加中显而易见。

充足的计算资源供应以及能够在链上验证计算的能力为链上人工智能代理打开了大门。代理是经过训练的模型，能够代表用户执行请求。代理提供了极大的机会来显著增强链上体验，使用户能够通过与聊天机器人交谈来执行复杂的交易。然而，就目前而言，代理项目仍集中于开发基础设施和工具，以便轻松快速地部署。

去中心化计算

概述

人工智能需要大量的计算资源，无论是用于训练模型还是进行推理。在过去的十年里，随着模型变得越来越复杂，计算需求呈指数级增长。例如，OpenAI 发现，在 2012 年至 2018 年间，其模型的计算需求从每两年翻倍增长到每三个半月翻倍增长。这导致了对 GPU 的需求激增，一些加密货币矿工甚至利用他们的 GPU 提供云计算服务。随着获取计算资源的竞争加剧和成本上涨，一些项目正在利用加密货币提供去中心化计算解决方案。它们以有竞争力的价格提供按需计算，以便团队可以负担得起训练和运行模型。在某些情况下，这种权衡可能是性能和安全性。

像 Nvidia 生产的最先进的 GPU 等高端硬件需求很高。在 9 月份，Tether 收购了德国比特币矿工 Northern Data 的股份，据报道支付了 4.2 亿美元，以收购 1 万个 H100 GPU（用于 AI 训练的最先进的 GPU 之一）。获得最佳硬件的等待时间至少为六个月，在许多情况下更长。更糟糕的是，公司通常需要签订长期合同，购买他们甚至可能不会使用的计算资源。这可能导致存在计算资源，但市场上却不可用的情况。去中心化计算系统有助于解决这些市场效率低下的问题，创建了一个二级市场，使计算资源的所有者能够随时以竞争价格出租他们的多余资源，释放新的供应。

除了竞争性定价和易获取性外，去中心化计算的关键价值是抗审查性。前沿的人工智能发展越来越被拥有无与伦比算力和数据获取权限的大型科技公司所主导。2023 年 AI 指数报告年度报告中首次突出的关键主题之一是，行业正在超越学术界，在 AI 模型的开发方面，将控制权集中在少数科技领导者手中。这引发了对他们能否在制定支撑 AI 模型的规范和价值观方面产生过大影响的担忧，尤其是在这些科技公司推动监管措施以限制他们无法控制的 AI 开发之后。

去中心化计算垂直领域

近年来出现了几种去中心化计算模型，每种模型都有自己的重点和取舍。

通用计算

类似 Akash、io.net、iExec、Cudos 等项目是去中心化计算应用，除了数据和通用计算解决方案外，还提供或将很快提供专门用于 AI 训练和推理的特定计算资源。

Akash 目前是唯一完全开源的「超级云」平台。它是一个使用 Cosmos SDK 的PoS网络。Akash 的原生代币 AKT 用于保护网络、作为支付形式，并激励参与。Akash 于 2020 年推出了首个主网，重点是提供一个无需许可的云计算市场，最初提供存储和 CPU 租赁服务。在 2023 年 6 月，Akash 推出了一个新的测试网，专注于 GPU，9 月推出了 GPU 主网，使用户能够租用 GPU 进行 AI 训练和推理。

Akash 生态系统中有两个主要角色 – 租户和提供者。租户是 Akash 网络的用户，他们想购买计算资源。提供者是计算资源提供方。为了匹配租户和提供者，Akash 依赖于一个逆向拍卖过程。租户提交他们的计算需求，在其中可以指定某些条件，比如服务器的位置或进行计算的硬件类型，以及他们愿意支付的金额。然后，提供者提交他们的要价，最低出价者获得任务。

Akash 验证者维护网络的完整性。验证者集目前限制为 100 个，计划随着时间逐步增加。任何人都可以通过质押比当前质押金额最少的验证者更多的 AKT 来成为验证者。AKT 持有者也可以将他们的 AKT 委托给验证者。网络的交易费用和区块奖励以 AKT 形式分配。此外，对于每笔租赁，Akash 网络都会以由社区确定的比率收取「手续费」，并分配给 AKT 持有者。

二级市场

去中心化计算市场旨在填补现有计算市场的低效。供应限制导致公司储备了超出他们可能需要的计算资源，而且由于与云服务提供商的合同形式，供应进一步受到限制。即使可能不需要持续使用，这些客户也被锁定在长期合同中。去中心化计算平台释放了新的供应，使全球任何需要的计算资源的人都可以成为提供方。

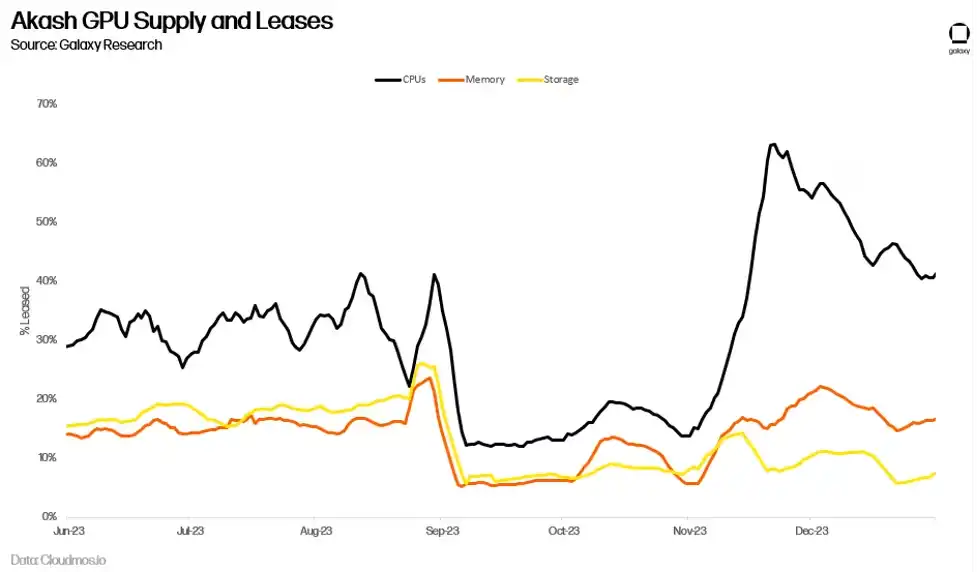
目前尚不清楚，对用于 AI 训练的 GPU 的需求激增是否会转化为 Akash 网络的长期使用量。长期以来，Akash 一直为 CPU 提供了一个市场，例如，以 70-80% 的折扣提供类似于中心化替代方案的服务。然而，更低的价格并没有导致显著的采用。网络上的租赁活动已经趋于平缓，2023 年第二季度的平均计算资源利用率仅为 33%，内存利用率为 16%，存储利用率为 13%。尽管这些对于链上采用来说是令人印象深刻的指标（作为参考，领先的存储提供商 Filecoin 在 2023 年第三季度的存储利用率为 12.6%），但这表明供应继续超过对这些产品的需求。

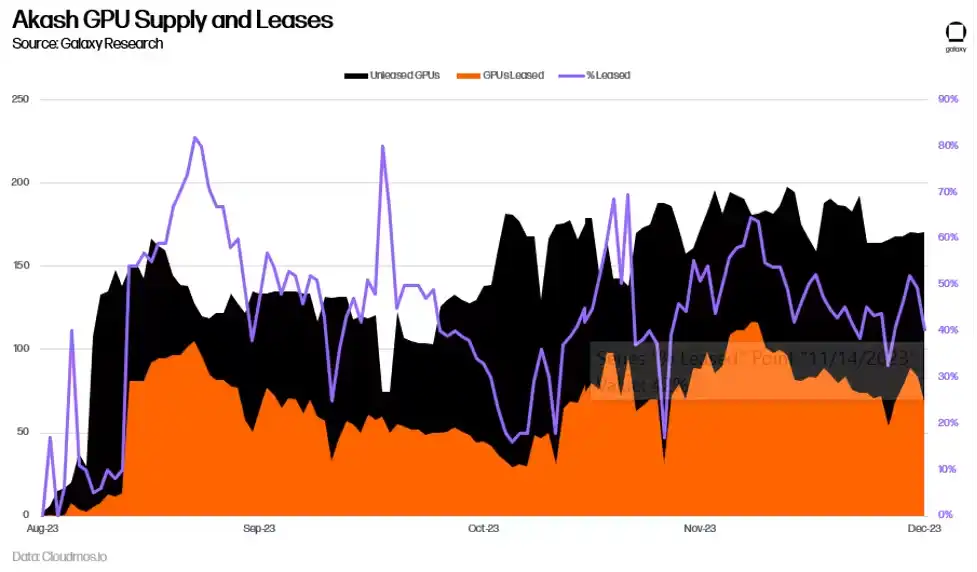
距离 Akash 推出 GPU 网络仅推出半年多的时间，现在准确衡量其长期采用率还为时过早。作为需求的标志，迄今为止 GPU 的平均利用率为 44%，高于 CPU、内存和存储。这主要是由对最高质量 GPU（如 A100s）的需求推动的，超过 90% 的高质量 GPU 已出租。

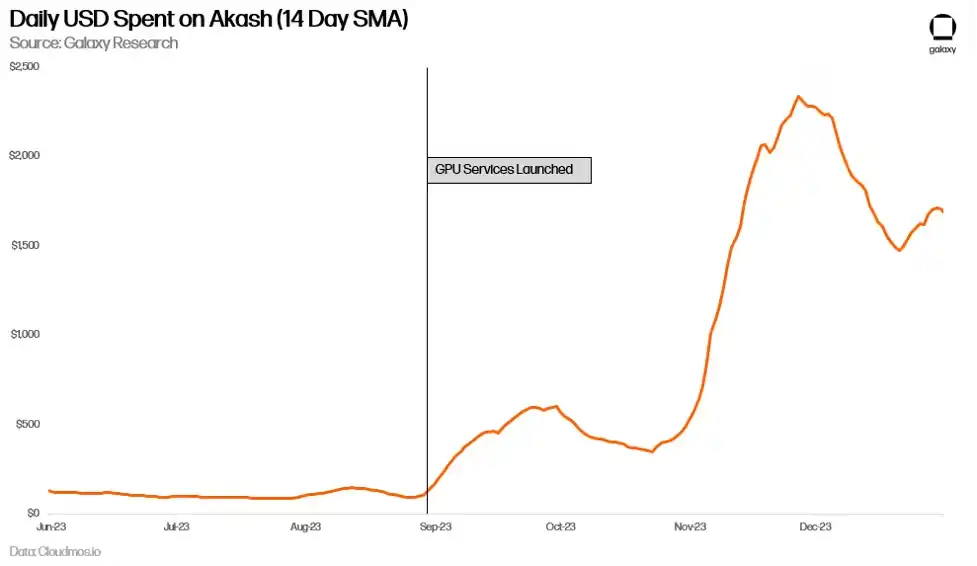
Akash 的每日支出也有所增加，相对于 GPU 出现之前几乎翻了一番。这部分归因于其他服务使用量的增加，尤其是 CPU，但主要还是新 GPU 导致的。

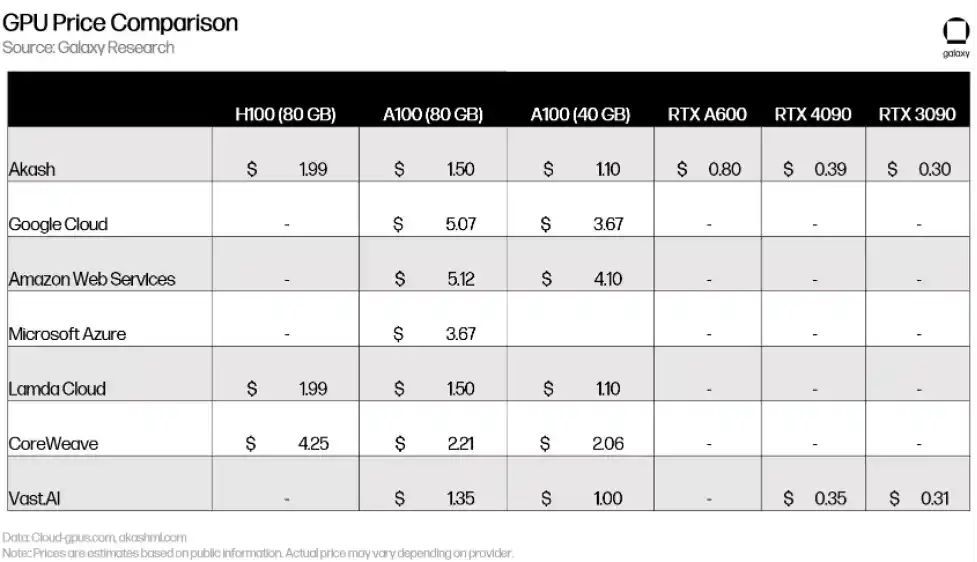
定价与 Lambda Cloud 和 Vast.ai 等中心化竞争对手相当（或者在某些情况下甚至更贵）。对最高端 GPU（例如 H100 和 A100）的巨大需求意味着该设备的大多数所有者对在面临竞争性定价的市场上市兴趣不大。

尽管初期令人欣喜，但采用仍然存在障碍（下文将进一步讨论）。去中心化计算网络需要采取更多措施来创造需求和供应，团队正在尝试如何更好地吸引新用户。例如，在 2024 年初，Akash 通过了提案 240，以增加 GPU 提供方的 AKT 释放，并激励更多的供应，具体针对高端 GPU。团队还致力于推出概念验证模型，向潜在用户展示其网络的实时能力。Akash 正在训练他们自己的基础模型，并已经推出了使用 Akash GPU 生成输出的聊天机器人和图像生成产品。类似地，io.net 已经开发了稳定的扩散模型，并正在推出新的网络功能，以更好地模拟传统 GPU 数据中心的性能和规模。

去中心化机器学习训练

除了可以满足人工智能需求的通用计算平台外，还出现了一系列专注于机器学习模型训练的专用 AI GPU 提供方。例如，Gensyn 正在「协调电力和硬件来构建集体智慧」，认为「如果有人想训练某些东西，而有人愿意训练它，那么应该允许进行训练。」

该协议有四个主要角色：提交者、求解者、验证者和举报者。提交者向网络提交带有训练请求的任务。这些任务包括训练目标、要训练的模型和训练数据。作为提交过程的一部分，提交者预先支付一笔费用，以支付求解者估计的计算成本。

一旦提交，任务将分配给求解者，他们将进行模型的实际训练。然后，求解者将完成的任务提交给验证者，验证者负责检查训练是否正确完成。举报者负责确保验证者诚实行事。为了激励举报者参与网络，Gensyn 计划定期提供有意错误的证明，以奖励举报者抓住它们。

除了为人工智能相关工作提供计算之外，Gensyn 的关键价值是其验证系统，该系统仍在开发中。验证是必要的，以确保 GPU 提供方进行的外部计算是正确的（即确保用户的模型被训练成他们想要的方式）。Gensyn 采用一种独特的方法解决了这个问题，利用称为「概率学习证明、基于图的定位协议和 Truebit 风格的激励游戏」的新型验证方法。这是一种乐观求解模式，使验证者能够确认求解者已正确运行模型，而无需完全重新运行它们，这是一种昂贵且低效的过程。

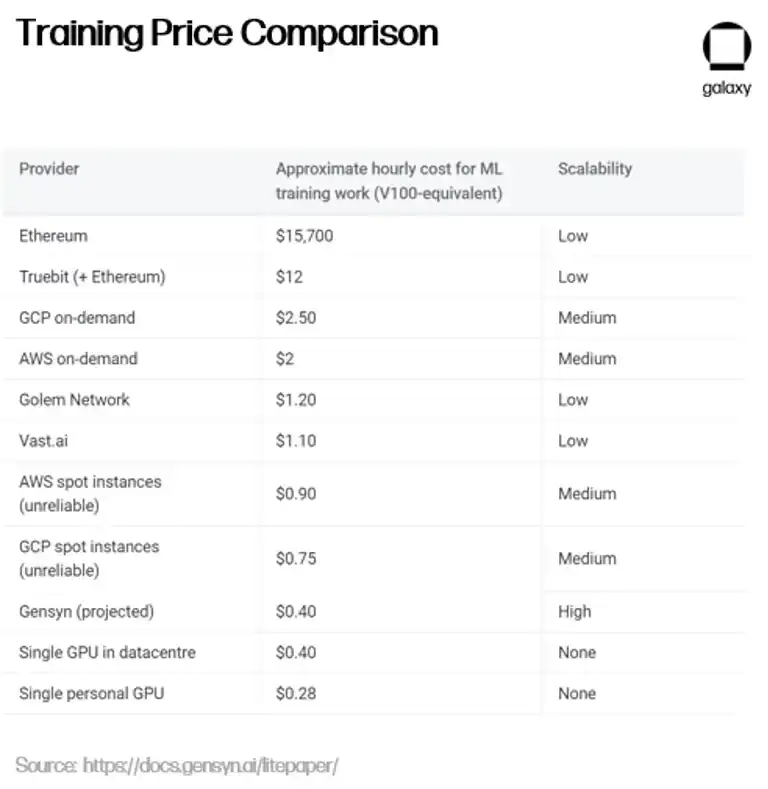
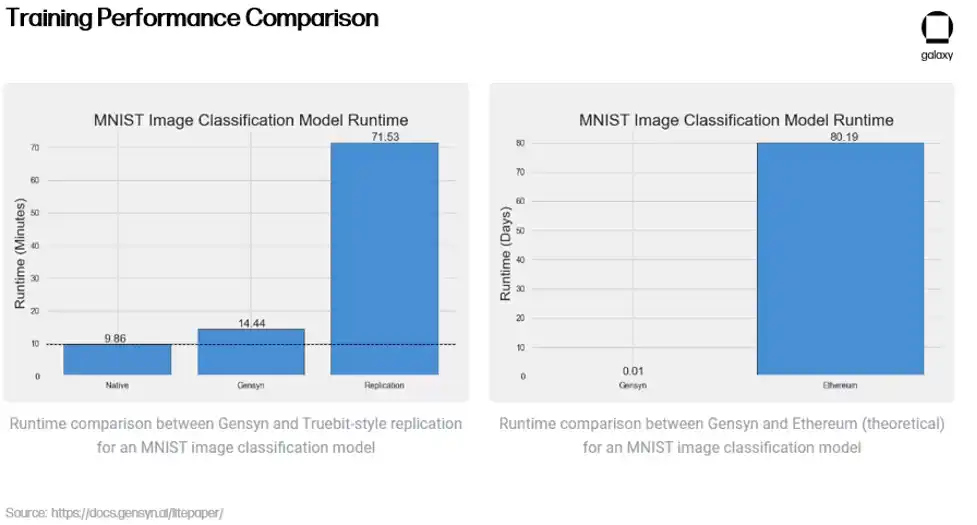
除了其创新的验证方法外，Gensyn 还声称相对于中心化替代方案和加密竞争对手来说具有成本效益 – 提供的 ML 训练比 AWS 便宜高达 80%，同时在测试中胜过类似项目 Truebit。

这些初步结果能否在去中心化网络中规模化复制，还有待观察。Gensyn 希望利用来自提供方（如小型数据中心、普通用户，甚至将来的小型移动设备，如手机）的多余计算资源。然而，正如 Gensyn 团队自己承认的，依赖异构计算提供方会引入几个新挑战。

对于像谷歌云和 Coreweave 这样的中心化提供方来说，计算是昂贵的，而计算之间的通信（带宽和延迟）是便宜的。这些系统旨在尽快实现硬件之间的通信。Gensyn 颠覆了这种框架，通过使世界上任何人都能够提供 GPU 来降低计算成本，但由于网络现在必须在去中心化的、位于遥远地方的异构硬件之间协调计算作业，从而增加了通信成本。Gensyn 尚未推出，但它证明了在构建去中心化机器学习训练协议时可能发生的事情。

去中心化通用人工智能

去中心化计算平台还为人工智能创建方法的设计可能性打开了大门。Bittensor 是一个建立在 Substrate 上的去中心化计算协议，试图回答「我们如何将人工智能转变为协作方式」的问题。Bittensor 旨在将人工智能生成去中心化和商品化。该协议于 2021 年推出，旨在利用协作式机器学习模型的力量，不断迭代和产生更好的人工智能。

Bittensor 从比特币中汲取灵感，其原生货币 TAO 的供应量为二千一百万，有一个四年的减半周期（首次减半将在 2025 年）。与使用工作量证明来生成正确的随机数并获得区块奖励不同，Bittensor 依赖于「智能证明（Proof of Intelligence）」，要求矿工运行能够对推理请求产生输出的模型。

智能激励网络

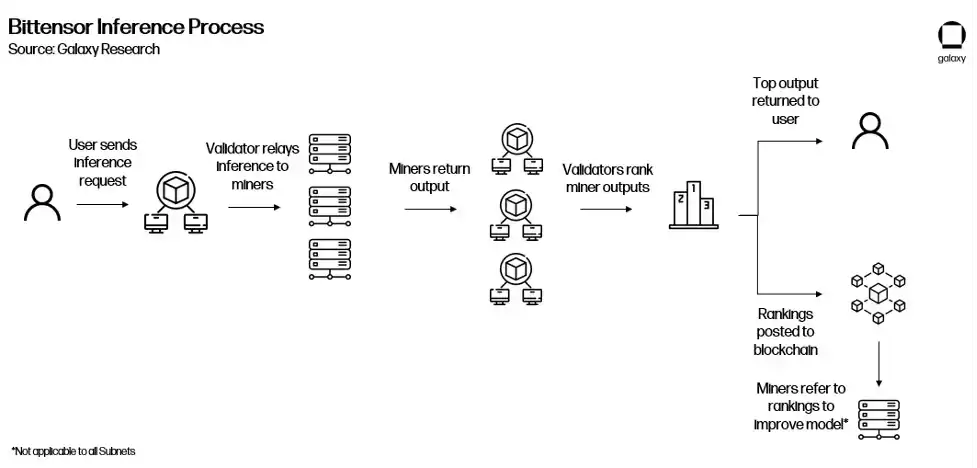
Bittensor 最初依赖混合专家（MoE）模型来生成输出。当推理请求被提交时，MoE 模型不是依赖于一个通用模型，而是将推理请求传递给针对特定输入类型最准确的模型。可以将其类比为建造房屋时，雇用各种专家来处理建造过程的不同方面（例如：建筑师、工程师、画家、建筑工人等…）。MoE 将其应用于机器学习模型，尝试根据输入利用不同模型的输出。正如 Bittensor 创始人 Ala Shaabana 所解释的那样，这就像「与一群聪明人，而不是与一个人交谈，以得到最好的答案」。由于确保正确路由、将消息同步到正确模型以及激励的挑战，这种方法已经被搁置，直到项目更为发展成熟。

Bittensor 网络中有两个主要角色：验证者和矿工。验证者负责向矿工发送推理请求，审查他们的输出，并根据其响应的质量对其进行排名。为了确保其排名可靠，验证者根据其排名与其他验证者排名的一致程度被赋予「vtrust」分数。验证者的 vtrust 分数越高，他们就能够获得更多的 TAO。这旨在鼓励验证者随着时间的推移就模型排名达成共识，因为达成对模型排名的共识的验证者越多，他们个人的 vtrust 分数就越高。

矿工，也称为服务器，是运行实际机器学习模型的网络参与者。矿工之间竞争，为给定查询提供最准确的输出，输出越准确，他们获得的 TAO 发行就越多。矿工可以以任何他们想要的方式生成这些输出。例如，在未来的场景中，一个 Bittensor 矿工完全可能事先在 Gensyn 上对模型进行训练，然后将其用于赚取 TAO。

如今大多数交互直接发生在验证者和矿工之间。验证者向矿工提交输入并请求输出（即对模型进行训练）。一旦验证者向网络中的矿工查询并收到他们的响应，然后他们对验证者进行排名并将其排名提交给网络。

验证者（依赖 PoS）和矿工（依赖 Proof of Model，一种 PoW 形式）之间的这种交互被称为 Yuma 共识。它旨在鼓励矿工产生最佳输出以赚取 TAO，以及鼓励验证者准确对矿工输出进行排名，以赚取更高的 vtrust 分数并增加他们的 TAO 奖励，形成网络的共识机制。

子网及应用

上文提到，Bittensor 上的交互主要包括验证者向矿工提交请求并评估其输出。然而，随着贡献矿工的质量提高和网络整体人工智能的增长，Bittensor 将在其现有堆栈之上创建一个应用程序层，使开发者能够构建查询 Bittensor 网络的应用程序。

在 2023 年 10 月，通过其 Revolution 升级，Bittensor 完成了朝着实现这一目标迈出的重要一步，引入了子网。子网是 Bittensor 上的个独立网络，激励特定行为。Revolution 将网络开放给任何有兴趣创建子网的人。自发布以来的几个月里，已经推出了超过 32 个子网，包括用于文本提示、数据抓取、图像生成和存储等领域的子网。随着子网的成熟和产品准备就绪，子网创建者还将创建应用程序集成，使团队能够构建查询特定子网的应用程序。一些应用程序（聊天机器人、图像生成器、推特回复机器人、预测市场）今天已经存在，但除了 Bittensor 基金会的拨款之外，验证者没有正式激励来接受和转发这些查询。

为了提供更清晰的说明，下图是 Bittensor 集成应用程序后可能运行的示例。

子网根据根网络评估的表现来获得 TAO。根网络位于所有子网的顶部，实质上充当一种特殊类型的子网，并由 64 个最大的子网验证者按份额管理。根网络验证者根据子网的表现对其进行排名，并定期向子网分配 TAO。这样，各个子网就充当了根网络的矿工。

Bittensor 前景

Bittensor 在扩展协议功能以激励跨多个子网的智能生成时，仍在经历成长的痛苦。矿工们继续想出新的方法来攻击网络，以赚取更多的 TAO，例如通过略微修改其模型运行的高评级推理的输出，然后提交多个变体。影响整个网络的治理提案只能由 Triumvirate 提交和实施，Triumvirate 完全由 Opentensor 基金会的利益相关者组成（值得注意的是，提案在实施之前需要 Bittensor 验证者审批）。项目的代币经济学正在进行改进，以改善 TAO 在子网中的使用激励。该项目还因其独特的方法而迅速出圈，最受欢迎的人工智能网站 HuggingFace 的 CEO 表示 Bittensor 应该将其资源添加到该网站中。

在一篇最近由核心开发者发布的名为「Bittensor Paradigm」的文章中，团队阐明了他们对 Bittensor 最终演变为「不受测量对象限制（agnostic to what is being measured）」的愿景。理论上，这可以使 Bittensor 开发激励任何类型行为的子网，所有这些都由 TAO 提供支持。然而，仍然存在相当大的实际约束 – 最主要的是要证明这些网络能够扩展到处理如此多样的过程，并且底层的激励机制推动的进展超过了中心化的提供。

构建用于 AI 模型的去中心化计算堆栈

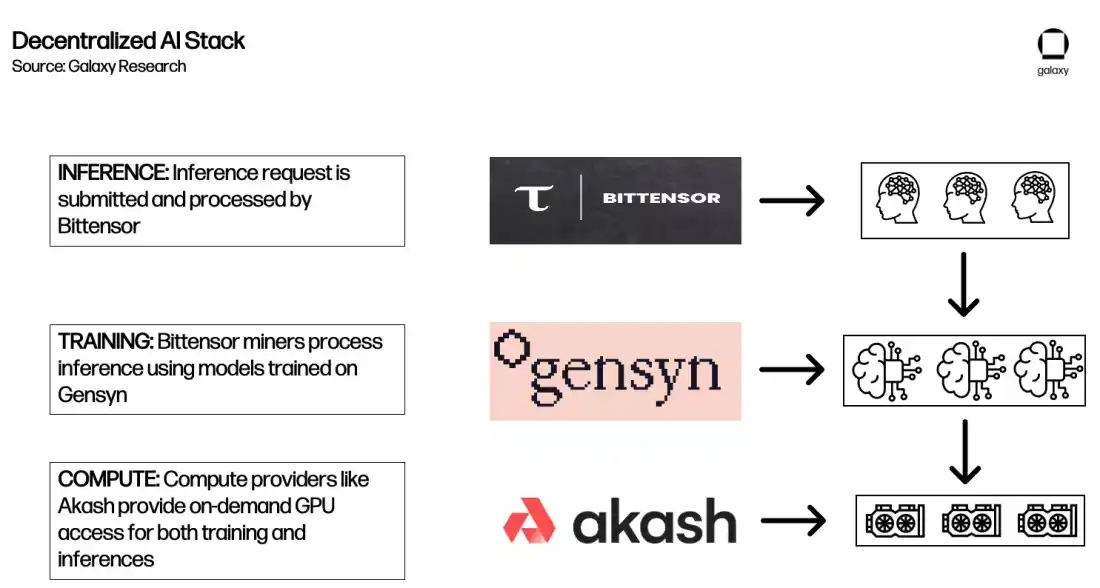
上述部分阐述了正在开发的各种类型的去中心化人工智能计算协议的框架。虽然它们在发展和采用方面还处于早期阶段，它们为生态系统提供了基础，该生态系统最终可能促进创建「AI 构建块」，就像「DeFi 乐高」概念一样。无需许可的区块链的可组合性开启了每个协议在其他协议之上构建的可能性，从而提供了更全面的去中心化人工智能生态系统。

例如，以下是 Akash、Gensyn 和 Bittensor 可能如何相互交互以响应推理请求的一种方式。

需要明确的是，这仅仅是未来可能发生事情的一个示例，而不是对当前生态系统、现有合作伙伴或可能结果。今天，互操作性的限制以及下文描述的其他考虑因素大大限制了集成可能性。除此之外，流动性的碎片化和使用多个代币的需求可能对用户体验产生不利影响，这一点已经被 Akash 和 Bittensor 的创始人指出。

其他去中心化产品

除了计算之外，还有几种其他去中心化基础设施服务，以支持加密货币新兴的人工智能生态系统。列举它们所有的内容超出了本报告的范围，但其中一些有趣而具有代表性的例子包括：

Ocean：去中心化的数据市场。用户可以创建代表其数据的数据 NFT，并使用数据代币购买。用户既可以将其数据货币化，又可以拥有更大的主权，同时为从事人工智能开发和训练模型的团队提供所需的数据获取途径。

Grass：去中心化的带宽市场。用户可以将他们多余的带宽出售给使用它从互联网上抓取数据的人工智能公司。该市场建立在 Wynd 网络上，这不仅使个人可以将其带宽货币化，而且还为带宽的购买者提供了更多样化的视角，了解个人用户在线上看到的内容（因为个人使用互联网访通常是针对其特定的 IP 地址）。

HiveMapper：构建一个去中心化的地图产品，其中包含从汽车驾驶员收集的信息。HiveMapper 依赖人工智能来解释用户汽车仪表板摄像头收集的图像，并通过强化人类学习反馈（RHLF）奖励用户帮助完善人工智能模型。

总的来说，这些都指向了探索支持人工智能模型的去中心化市场模型，或者支持开发这些模型所需的周边基础设施的近乎无尽的机会。目前，这些项目大多处于概念验证阶段，需要进行更多的研究和开发，以证明它们能够以所需的规模提供全面的人工智能服务。

展望

去中心化计算产品仍处于开发的早期阶段。他们刚刚开始使用最先进的计算能力，训练生产环境中最强大的人工智能模型。为了获得有意义的市场份额，他们需要展示与中心化替代品相比的实际优势。更广泛采用的潜在诱因包括：

GPU 供需情况。GPU 供应短缺，加上快速增长的计算需求，导致了一场 GPU 竞赛。由于 GPU 有限，OpenAI 已经限制了对其平台的使用。像 Akash 和 Gensyn 这样的平台可以为需要高性能计算的团队提供成本竞争力的替代方案。未来 6-12 个月是去中心化计算提供方吸引新用户的特殊机会，因为这些用户被迫考虑去中心化方案。加上越来越高效的开源模型（如 Meta 的 LLaMA 2），用户在部署有效的微调模型时不再面临同样的障碍，这让计算资源成为主要瓶颈。然而，平台本身的存在并不能确保计算资源的充足供应和消费者的对应需求。获得高端 GPU 仍然困难，而成本并不总是需求方的主要动机。这些平台将面临挑战，要证明使用去中心化计算的实际好处 – 无论是因为成本、抗审查性、持续时间和弹性还是可使用性 – 以积累粘性用户。那么这些协议不得不行动迅速。GPU 基础设施的投资和建设速度非常惊人。

监管。监管继续是去中心化计算运动的一大障碍。在短期内，缺乏明确的监管意味着提供方和用户使用这些服务面临潜在的风险。如果提供方无意中提供计算或买家从受制裁的实体购买计算，会怎么样？用户可能不愿使用缺乏中心化实体控制和监督的去中心化平台。协议已经试图通过将控制纳入其平台或仅提供已知计算提供方的筛选器（即提供 KYC 信息）来缓解这些担忧，但需要更加强大的方法来保护隐私同时确保合规，以促进采用。短期内，我们可能会看到出现 KYC 和符合监管的平台，限制对其协议的使用以解决这些问题。

审查。监管是双向的，去中心化计算提供方可能受益于限制对人工智能的使用所采取的行动。除了行政命令外，OpenAI 创始人 Sam Altman 曾在国会作证，强调了颁发人工智能开发许可证的监管机构的必要性。围绕人工智能监管的讨论刚刚开始，但任何试图限制对人工智能的使用或审查人工智能的尝试可能会加速采用没有这些障碍的去中心化平台。去年 11 月 OpenAI 的领导层变动进一步证明了将决策权授予仅有少数人的最强大的现有人工智能模型存在的风险。此外，所有人工智能模型都必然反映了其创建者的偏见，无论是有意还是无意。消除这些偏见的一种方法是尽可能地使模型对微调和训练开放，确保任何人都可以随时随地使用各种偏见的模型。

数据隐私。当与为用户提供数据自主权的外部数据和隐私解决方案集成时，去中心化计算可能会比替代方案更具吸引力。三星公司就曾遭受此类问题，他们意识到工程师正在使用 ChatGPT 来帮助芯片设计，并泄露了敏感信息给 ChatGPT。Phala Network 和 iExec 声称为用户提供了 SGX 安全隔离区，以保护用户数据，并且正在进行完全同态加密的研究，进一步解锁确保隐私的去中心化计算。随着人工智能进一步融入我们的生活，用户将更加重视能够在具有隐私保护功能的应用程序上运行模型。用户还将需求能够实现数据的可组合性，以便能够无缝地将其数据从一个模型转移到另一个模型。

用户体验（UX）。用户体验仍然是所有类型的加密应用和基础设施更广泛采用的重要障碍。去中心化计算方案也不例外，并且在某些情况下，由于开发者需要理解加密和人工智能，这种情况更加严重。需要进行改进的方面包括从入门和与区块链交互的抽象到提供与当前市场领导者相同的高质量输出。这是显而易见的，因为许多运行中的去中心化计算协议提供更便宜的方案，但难以获得常规使用。

智能合约与零知识机器学习（zkML）

智能合约是任何区块链生态系统的核心之一。在特定条件下，它们会自动执行并减少或消除对可信第三方的需求，从而实现了像 DeFi 中所见的复杂去中心化应用程序的创建。然而，就目前而言，智能合约在功能上仍然存在局限性，因为它们基于预设参数执行，这些参数必须进行更新。

例如，一个借贷协议智能合约根据一定的贷款价值比例规范了何时清算头寸。在一个风险不断变化的动态环境中，这些智能合约必须不断更新以考虑风险容忍度的变化，这为通过去中心化流程进行管理的合约带来了挑战。例如，依赖去中心化治理流程的 DAO 可能无法及时对系统性风险做出反应。

集成人工智能（如机器学习模型）的智能合约是增强功能、安全性和效率的一种可能的方式，同时改善整体用户体验。然而，这些集成也引入了额外的风险，因为无法确保支持这些智能合约的模型不会被攻击或考虑到长尾情况（众所周知，由于缺乏数据输入，很难对模型进行训练）。

零知识机器学习（zkML）

机器学习需要大量计算资源来运行复杂模型，这使得 AI 模型无法在智能合约内部直接运行，因为高昂的成本。例如，一个 DeFi 协议为用户提供了收益优化模型的功能，但如果试图在链上运行该模型，就必须支付高昂的 Gas 费。一种解决方案是增加底层区块链的计算能力。然而，这也会增加链的验证节点的负担，可能会削弱其去中心化属性。因此，一些项目正在探索使用 zkML 来以无需密集的链上计算就能以无许信任的方式验证输出的方法。

说明 zkML 有用性的一个常见示例是，当用户需要其他人通过模型运行数据，并验证其交易对手是否实际运行了正确的模型时。也许开发者正在使用去中心化计算提供方来训练他们的模型，担心提供方正在尝试通过使用成本更低的模型来节省成本，但输出几乎无法察觉。zkML 使得计算提供方可以运行数据通过他们的模型，然后生成一个证明，可以在链上验证模型对给定输入的输出是正确的。在这种情况下，模型提供者将有额外的优势，即能够提供他们的模型，而无需透露产生输出的底层权重。

相反的情况也可以发生。如果用户想要运行一个模型，使用他们的数据，但又不想让提供模型的项目获取他们的数据，因为存在隐私问题（例如医学检查或专有业务信息），那么用户可以在他们的数据上运行模型而不共享它，并验证他们是否运行了正确的模型，同时提供证据。这些可能性大大扩展了通过解决限制性计算限制来集成人工智能和智能合约功能的设计空间。

基础设施与工具

鉴于 zkML 领域的早期状态，开发主要集中在构建团队将其模型和输出转换为可在链上验证的证明所需的基础设施和工具上。这些产品尽可能地抽象了开发中的零知识方面。

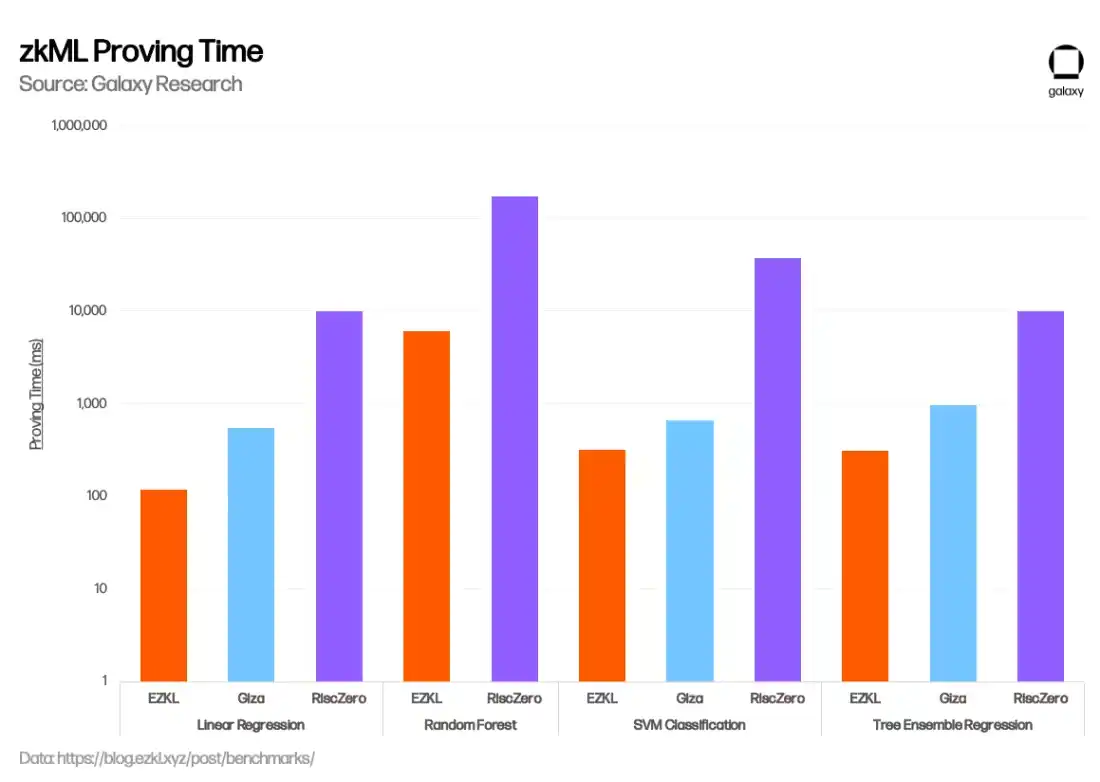
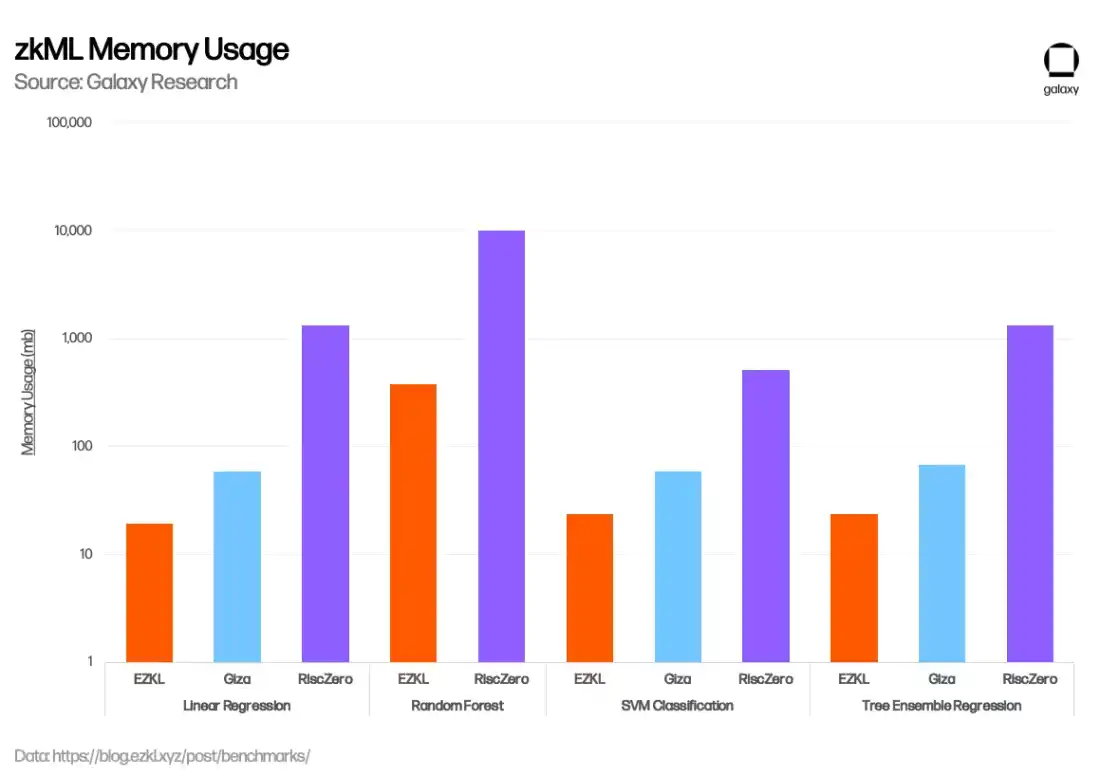
EZKL 和 Giza 这两个项目，通过提供机器学习模型执行的可验证证明，来构建这些工具。两者都帮助团队构建机器学习模型，以确保这些模型可以以一种无需信任地在链上验证结果的方式执行。这两个项目都使用开放式神经网络交换（ONNX）将用通用语言如 TensorFlow 和 Pytorch 编写的机器学习模型转换为标准格式。然后，在执行时它们输出这些模型的版本，也产生 zk-proofs。EZKL 是开源的，生成 zk-SNARKS，而 Giza 是闭源的，生成 zk-STARKS。这两个项目目前仅与 EVM 兼容。

在过去几个月中，EZKL 在增强其 zkML 解决方案方面取得了显著进展，主要集中在降低成本、提高安全性和加速证明生成方面。例如，在 2023 年 11 月，EZKL 集成了一个新的开源 GPU 库，将总体证明时间减少了 35%，并且在 1 月份，EZKL 宣布了 Lilith，这是一个软件解决方案，用于在使用 EZKL 证明系统时集成高性能计算集群并协调并发作业。Giza 独特之处在于，除了提供创建可验证机器学习模型的工具之外，他们还计划实现 Hugging Face 的 web3 等效版本，为 zkML 协作和模型共享开设一个用户市场，并最终集成去中心化的计算产品。在 1 月份，EZKL 发布了一个基准评估，比较了 EZKL、Giza 和 RiscZero（下文讨论）的性能。EZKL 表现出更快的证明时间和内存使用率。

Modulus Labs 也正在开发一种专为人工智能模型量身定制的新的 zk-proof 技术。Modulus 发表了一篇名为《The Cost of Intelligence》（暗示了在链上运行 AI 模型的成本极高）的论文，对当时的现有 zk-proofs 系统进行了基准测试，以识别改进 AI 模型 zk-proofs 的能力和瓶颈。该论文发表于 2023 年 1 月，表明现有的解决方案成本和效率都太高，无法实现大规模的 AI 应用。基于他们的初步研究，Modulus 在 11 月推出了 Remainder，这是一个专门为降低 AI 模型成本和证明时间而构建的专业零知识证明器，旨在使项目能够经济上可行地大规模集成模型到他们的智能合约中。他们的工作是闭源的，因此无法与上述解决方案进行基准测试，但最近在 Vitalik 的有关加密和人工智能的博客文章中提到了它们。

工具和基础设施的开发对 zkML 领域的未来增长至关重要，因为它极大地减少了团队部署 zk 电路以进行可验证的链下计算所需的摩擦力。创建安全接口，使非加密原生开发者在机器学习领域工作时能够将他们的模型带到链上，将使具有真正新颖用例的应用程序的实验增加。工具还解决了更广泛的 zkML 采用的一个主要障碍，即缺乏在零知识、机器学习和密码学交叉领域有知识和兴趣的开发者。

协处理器

正在开发的其他解决方案，称为「协处理器」，包括 RiscZero、Axiom 和 Ritual。术语「协处理器」在大多数情况下是语义上的 – 这些网络承担许多不同的角色，包括在链上验证链下计算。与 EZKL、Giza 和 Modulus 一样，它们的目标是完全抽象化零知识证明生成过程，从而创建基本上是能够在链下执行程序并为链上验证生成证明的零知识虚拟机。RiscZero 和 Axiom 可以处理简单的 AI 模型，因为它们是更通用的协处理器，而 Ritual 则专为与 AI 模型配合使用而构建。

Infernet 是 Ritual 的第一个实例，并包含一个 Infernet SDK，允许开发者向网络提交推理请求，并在返回时收到输出和证明（可选）。Infernet 节点接收这些请求，并在链下处理计算，然后返回输出。例如，一个 DAO 可以创建一个流程，以确保所有新的治理提案在提交之前满足某些先决条件。每次提交新提案时，治理合约都会通过 Infernet 触发推理请求，调用一个特定于 DAO 的治理训练过的 AI 模型。该模型审查提案，以确保提交了所有必要的条件，并返回输出和证明，要么批准，要么否决提案的提交。

在未来一年内，Ritual 团队计划推出构成基础设施层的附加功能，称为 Ritual Superchain。之前讨论过的许多项目都可以作为服务提供方插入到 Ritual 中。目前，Ritual 团队已经与 EZKL 整合进行了证明生成，并可能很快会添加来自其他领先提供方的功能。Ritual 上的 Infernet 节点还可以使用 Akash 或 io.net GPU，并查询在 Bittensor 子网上训练的模型。他们的最终目标是成为开放 AI 基础设施的首选提供方，能够为任何网络上的任何工作提供机器学习和其他与 AI 相关的任务服务。

应用

zkML 有助于调和区块链和人工智能之间的矛盾，前者天生资源受限，后者需要大量的计算和数据。正如 Giza 的一位创始人所说：「用例是如此丰富… 这有点像在以太坊早期问智能合约有哪些用例一样… 我们正在扩展智能合约的用例。」然而，正如上文所强调的，当今的发展主要集中在工具和基础设施层面。应用程序仍处于探索阶段，团队们面临的挑战是证明使用 zkML 实现模型带来的价值超过了这样做的复杂性和成本。

今天的一些应用包括：

DeFi。zkML 通过增强智能合约的功能，拓展了 DeFi。DeFi 协议为机器学习模型提供了大量可验证和不变的数据，可用于生成产生收益或交易策略、风险分析、UX 等。例如，Giza 与 Yearn Finance 合作，为 Yearn 的新 v3 保险库构建了一个概念验证的自动风险评估引擎。Modulus Labs 与 Lyra Finance 合作，将机器学习纳入其 AMMs，与 Ion Protocol 合作验证者风险模型，并帮助 Upshot 验证其基于 AI 的 NFT 价格数据源。像 NOYA（利用 EZKL）和 Mozaic 这样的协议提供了对专有链下模型的使用，使用户能够使用自动 APY 机枪池，同时能够在链上验证数据输入和证明。Spectral Finance 正在构建链上信用评分引擎，预测 Compound 或 Aave 借款人违约的可能性。这些所谓的「De-Ai-Fi」产品有望在未来几年中变得更加普遍，这要归功于 zkML。

游戏。人们一直认为区块链颠覆和增强游戏的时机已经成熟。zkML 使得在链上使用人工智能进行游戏成为可能。Modulus Labs 已经为简单的链上游戏实现了概念验证。Leela vs the World是一个博弈论象棋游戏，用户与 AI 象棋模型对决，zkML 验证 Leela 的每一步都是基于游戏所采用的模型在运行。类似地，团队们使用 EZKL 框架构建了简单的唱歌比赛和链上井字棋。Cartridge 正在利用 Giza 使团队能够部署完全在链上的游戏，最近力推了一个简单的 AI 驾驶游戏，用户竞争创建更好的模型，使汽车避开障碍物。虽然简单，但这些概念验证指向了未来的落地，即实现更复杂的链上验证，如与 AI Arena 中的高级 NPC 角色交互的游戏经济相互作用，AI Arena 是一款类似于超级马里奥的游戏，玩家训练自己的战士，然后部署为 AI 模型进行战斗。

身份、溯源和隐私。加密已经被用作验证真实性的手段，并对越来越多的 AI 生成/操纵的内容和深伪进行打击。zkML 可以推进这些努力。WorldCoin 是一个人格证明的解决方案，需要用户扫描他们的虹膜生成唯一 ID。未来，生物识别 ID 可以通过使用加密存储在个人设备上自我保管，所需的模型用于本地验证这些生物识别信息。用户可以提供他们的生物识别信息的证明，而无需透露自己的身份，从而抵御女巫攻击，同时确保隐私。这也可以应用于其他需要隐私的推断，例如使用模型分析医学数据/图像以检测疾病、验证个体身份并在约会应用程序中开发匹配算法，或用于需要验证财务信息的保险和贷款机构。

展望

zkML 仍处于实验阶段，大多数项目都专注于构建基础设施原型和概念验证。目前面临的挑战包括计算成本、内存限制、模型复杂性、有限的工具和基础设施，以及开发人才。简而言之，在 zkML 可以实现消费产品所需的规模之前，还有大量工作要做。

然而，随着领域的成熟和这些限制的解决，zkML 将成为人工智能和加密集成的关键组成部分。在其核心，zkML 承诺能够将任何规模的链下计算带到链上，同时保持与在链上运行计算相同或接近相同的安全保障。然而，在实现这一愿景之前，该技术的早期用户将继续不得不在 zkML 的隐私和安全性与替代方案的效率之间进行权衡。

人工智能代理

人工智能和加密货币最令人兴奋的集成之一是正在进行的人工智能代理实验。代理是能够接收、解释和执行任务的自治机器人，使用的是 AI 模型。代理可以是任何东西，从拥有一个始终可用、根据您的偏好进行优化的个人助手，到雇佣一个财务代理，根据用户的风险偏好管理，并调整投资组合。

代理和加密很好地结合在一起，因为加密提供了无需许可和无需信任的支付基础设施。一旦训练完成，代理可以拥有一个钱包，以便它们可以自行与智能合约进行交易。例如，如今简单的代理可以在互联网上搜索信息，然后根据一个模型在预测市场上进行交易。

代理提供商

Morpheus 是 2024 年在以太坊和 Arbitrum 上推出的最新的开源代理项目之一。其白皮书于 2023 年 9 月匿名发布，为一个社区形成和建立提供了基础（包括像 Erik Vorhees 这样的知名人物）。白皮书包括可下载的智能代理协议，这是一个开源的 LLM，可以在本地运行，由用户的钱包管理，并与智能合约进行交互。它使用智能合约排名来帮助代理确定基于诸如处理的交易数量等标准与哪些智能合约进行交互是安全的。

白皮书还提供了构建 Morpheus 网络的框架，例如实施智能代理协议所需的激励结构和基础设施。这包括激励贡献者为与代理交互的前端构建界面，为开发者构建可以插入代理以便它们彼此交互的应用程序的 API，以及为用户提供云解决方案，以便他们可以使用在边缘设备上运行代理所需的计算和存储。该项目的初始资金于 24 年 2 季度初启动，完整的协议预计将在那时推出。

去中心化自治基础设施网络 (DAIN) 是一种新的代理基础设施协议，在 Solana 上构建代理到代理经济。DAIN 的目标是让来自不同企业的代理可以通过通用 API 无缝地相互交互，从而大大开放 AI 代理的设计空间，重点是实现能够与 web2 和 web3 产品交互的代理。一月份，DAIN 宣布与 Asset Shield 首次合作，使用户能够将「代理签名者」添加到其多重签名中，这些签名者能够根据用户设置的规则解释交易并批准/拒绝。

Fetch.AI 是最早部署的人工智能代理协议之一，已经开发了一个生态系统，用于在链上使用其 FET 代币和 Fetch.AI 钱包构建、部署和使用代理。该协议提供了一套全面的工具和应用程序，用于使用代理，包括与代理进行交互和下达命令的钱包内功能。

Autonolas 的创始人来自 Fetch 团队的前成员，他们是一个用于创建和使用去中心化的人工智能代理的开放市场。Autonolas 还为开发者提供一套工具，用于构建链下托管的人工智能代理，并能够连接到包括 Polygon、以太坊、Gnosis Chain 和 Solana 在内的多条链。他们目前有一些活跃的代理概念验证产品，包括用于预测市场和 DAO 治理的产品。

SingularityNet 正在建立一个用于 AI 代理的去中心化市场，人们可以在那里部署专注于特定领域的 AI 代理，这些代理可以被其他人或代理雇佣来执行复杂的任务。其他项目，如 AlteredStateMachine，正在构建与 NFTs 的 AI 代理集成。用户铸造具有随机属性的 NFTs，这些属性使它们对不同任务具有优势和劣势。然后，这些代理可以被训练来增强某些属性，用于游戏、DeFi 或作为虚拟助手，并与其他用户进行交易。

总的来说，这些项目设想了一个代理的未来生态系统，这些代理能够共同工作，不仅执行任务，还能帮助构建人工通用智能。真正复杂的代理将能够自主地执行任何用户任务。例如，不需要确保代理已经集成了外部 API（如旅行预订网站）就可以使用它，完全自主的代理将有能力找出如何雇佣另一个代理来集成 API，然后执行任务。从用户的角度来看，没有必要检查代理是否能够执行任务，因为代理可以自行确定。

比特币和人工智能代理

2023 年 7 月，闪电实验室推出了在闪电网络上使用代理的概念验证方案，称为 LangChain 比特币套件。这个产品尤其有趣，因为它旨在解决 Web 2 世界中一个日益严重的问题——网络应用程序的门禁（限制获取）和昂贵的 API 服务。

LangChain 通过为开发者提供一套工具，使代理能够购买、出售和持有比特币，以及查询 API 密钥并发送微支付来解决这个问题。在传统的支付渠道上，由于费用问题，小额微支付基本上不可行，而在闪电网络上，代理可以每天发送无限的微支付，并且只需支付极少的费用。当与 LangChain 的 L402 支付计量 API 框架结合使用时，这可以使公司根据使用量的增加和减少来调整对其 API 的使用费用，而不是设置一个单一的成本禁止标准。

在未来，链上活动主要由代理与代理交互所主导，上文提到的事情将是必要的，以确保代理能够以不成本过高的方式相互交互。这是一个早期的例子，说明如何在无需许可且经济高效的支付轨道上使用代理，为新市场和经济互动开辟了可能性。

展望

代理领域仍处于初期阶段。

项目刚刚开始推出功能代理，可以使用其基础设施处理简单的任务——这通常只有经验丰富的开发者和用户才能使用。

然而，随着时间的推移，人工智能代理将对加密领域产生的最大影响之一是改善所有垂直领域的用户体验。交易将开始从基于点击转向基于文本，用户将能够通过大语言模型（LLMs）与链上代理进行交互。已经有像 Dawn Wallet 这样的团队推出了用于用户在链上进行交互的聊天机器人钱包。

此外，尚不清楚代理在 Web 2.0 中如何运作，因为金融轨道依赖于受监管的银行机构，这些机构不能 24/7 运营且无法进行无缝跨境交易。正如 Lyn Alden 所强调的那样，因为缺乏退款和处理小额交易的能力，与信用卡相比，加密渠道尤其吸引人。然而，如果代理变得更普遍，现有的支付提供商和应用程序可能会迅速采取行动，实现所需的基础设施，使其能够在现有的金融渠道上运作，从而减轻使用加密的一些好处。

目前，代理可能仅限于确定性的加密货币交易，其中给定输入保证给定输出。如何利用这些代理的能力来执行复杂任务的模型，以及扩展其可以完成的任务范围的工具，都需要进一步的发展。要使加密代理在新颖的链上加密用例之外变得有用，需要更广泛地整合和接受加密作为支付形式以及法规的明确。然而，随着这些组件的发展，代理将成为上文讨论的去中心化计算和 zkML 解决方案中最大的消费者之一，以自主的非确定性方式接收和解决任何任务。

结论

人工智能向加密领域引入了与我们已经在 Web2 中看到的相同的创新，增强了从基础设施开发到用户体验和可使用性的各个方面。然而，项目仍处于早期阶段，在短期内，加密和人工智能的整合将主要由链下整合主导。

像 Copilot 这样的产品将「使开发效率提升 10 倍」，与微软等主要公司合作，Layer 1 们和 DeFi 应用程序已经在推出 AI 辅助开发平台。像 Cub3.ai 和 Test Machine 这样的公司正在开发用于智能合约审计和实时威胁监控的人工智能，以增强链上安全性。而 LLM 聊天机器人正在使用链上数据、协议文件和应用程序进行训练，以提供用户增强的可使用性和用户体验。

对于更高级的整合，真正充分利用加密的基础技术，挑战在于证明在链上实现人工智能解决方案在技术上是可行的，且在规模上是经济可行的。去中心化计算、zkML 和人工智能代理的发展都指向了有前景的垂直领域，为一个将加密和人工智能深度交织在一起的未来奠定了基础。